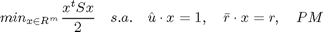
Dr. René J. Meziat, Departamento de Matemáticas, Universidad de los Andes, Bogotá, Colombia.
septiembre del 2006
Utlizaremos la función xlsread para leer la información de una hoja de cálculo tipo Exel. Este procedimiento será de gran utilidad dado que la mayoría de datos financieros provienen de manejadores de bases de datos comerciales. Comenzaremos por leer una matriz de covarianzas S de una hoja de cálculo.
[S,TXT,RAW]=XLSREAD('prueba');
S
Warning: Could not find an exact (case-sensitive) match for 'XLSREAD'. C:\Archivos de programa\MATLAB704\toolbox\matlab\iofun\xlsread.m is a case-insensitive match and will be used instead. You can improve the performance of your code by using exact name matches and we therefore recommend that you update your usage accordingly. Alternatively, you can disable this warning using warning('off','MATLAB:dispatcher:InexactMatch').
S =
0.2060 0.0375 0.1077 0.0493 0.0208 0.0059
0.0375 0.0790 0.0355 0.1028 0.0089 0.0406
0.1077 0.0355 0.0867 0.0443 0.0194 0.0148
0.0493 0.1028 0.0443 0.4435 0.0193 0.0274
0.0208 0.0089 0.0194 0.0193 0.0083 -0.0015
0.0059 0.0406 0.0148 0.0274 -0.0015 0.0392
Para efectos de este análisis consideraremos los datos estadísticos de los activos de las siguientes compañías:
tomados a partir de diez medidas de rendimiento continuo compuesto, tomadas entre 1974 y 1983. Datos obtenidos del texto de S. Benninga, p. 151, presentado en las referencias.
A continuación leemos un vector con los retornos medios R de los activos del análisis. Ellos se tomarán de la "segunda hoja" de la hoja de cálculo llamada prueba.
[R,TXT,RAW]=XLSREAD('prueba','Hoja2'); R
R =
0.2032
0.0531
0.1501
0.1529
0.1025
0.1210
Acorde a la literatura especializada (ver referencias al final de este informe), para determinar los portafolios óptimos acorde a un criterio de mínimo riesgo para un rendimento dado r, debemos resolver el siguiente programa matemático, que tiene función objetivo cuadrática convexa y restricciones lineales:
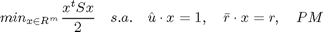
Donde
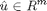
es un vector compuesto de sólo unos, el cual podemos construir a partir del vector de datos leido R, utilizando la siguiente instrucción abreviada:
u=R*0+1
u =
1
1
1
1
1
1
Los parámetros de la teoría son cuatro cantidades denominadas A, B, C y D. Definidas como formas cuadráticas a partir de la inversa de la matriz de covarianzas S.
Estas son:

Empleando Matlab calculamos estas cantidades de manera inmediata. Note el papel de la función inv para invertir matrices y el papel de la operación traspuesta que se realiza con el apóstrofe, por ejemplo: A' es la traspuesta de la matriz A. Así tenemos que:
A=u'*(inv(S)*u) B=u'*(inv(S)*R) C=R'*(inv(S)*R) D=A*C-B^2
A =
488.0546
B =
56.3000
C =
6.8676
D =
182.0762
Claramente D no es una forma cuadrática, pero proviene del determinante de las dos ecuaciones lineales que permiten hallar los multiplicadores de Lagrange en el problema matemático -PM-.
Para resolver el programa cuadrático convexo dado en -PM-, tomamos su función Lagrangiana:
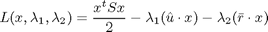
que podemos derivar e igualar a cero como es usual en optimización, para obtener las siguientes ecuaciones descritas en forma vectorial:
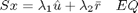
Multiplicando por la inversa de la matriz de covarianzas S, por la izquierda, sobre ambos lados de la ecuación -EQ- encontramos:

y utilizando las ecuaciones:

que provienen de las restricciones del programa -PM-, encontramos la siguiente pareja de ecuaciones lineales, cuyas incógnitas son los multiplicadores de Lagrange del programa -PM-. Así tenemos:

cuya solución da lugar a las siguientes expresiones:

las cuales a su vez permiten encontrar explícitamente el vector de inversiones x mediante las relaciones -SL- dadas más arriba.
Una vez hemos estimado los parámetros A, B, C y D del problema, procedemos a delinear la frontera eficiente, para ello utilizamos la fórmula explícita:
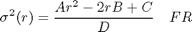
que se obtiene multiplicando por la traspuesta del vector óptimo x, por el lado izquierdo, ambos lados de la ecuación -EQ-.
Utilizando la fórmula -FR- podemos delinear sobre una gráfica de riesgo contra retorno la frontera eficiente que corresponde a los portafolios óptimos, que podemos formar con los activos de nuestro mercado de capitales.
Creamos un vector de 100 posiciones con los 100 valores, igualmente espaciados, que podemos tomar entre cero y un rango apropiado para el retorno máximo de nuestro análisis, que aquí tomaremos como el doble del máximo retorno medio de los activos disponibles.
x=linspace(0,2*max(R)); y=(A*x.^2-2*B*x+C)/D; plot(y,x) xlabel('riesgo como varianza') ylabel('retorno') title('frontera eficiente')
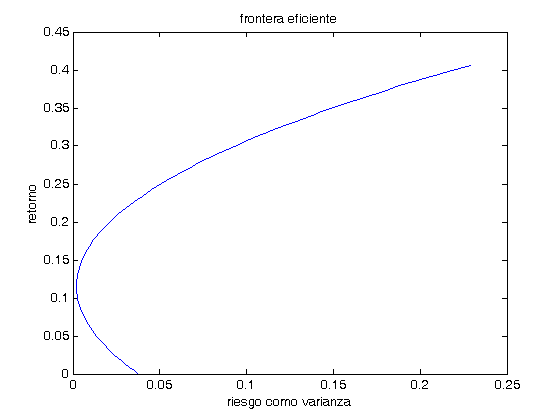
Sobre el mismo dibujo de la frontera eficiente, pondremos los activos que conforman nuestro mercado de acuerdo a sus medidas de riesgo y rendimiento, señalando que el riesgo lo medimos con la varianza de cada activo. Note que la varianza del activo -i- ocupa la -i-ésima posición en la diagonal de la matriz de covarianzas, esta es S(i,i).
hold on DTA=['A';'B';'G';'I';'P';'U']; for i=1:6 plot(S(i,i),R(i),'+g') text(S(i,i)+0.01,R(i),DTA(i)) end
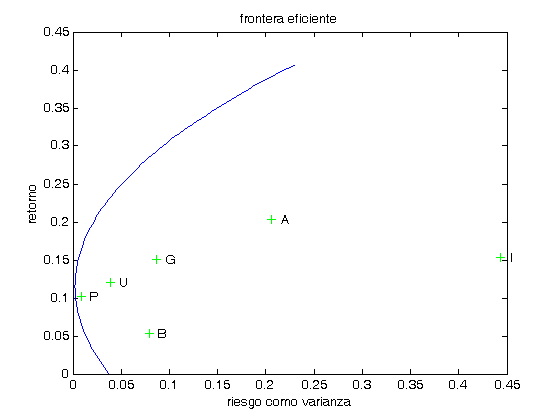
Con los parámetros A y B de la teoría, podemos señalar de una forma muy clara el vértice de la frontera eficiente. Usted debe observar que la ecuación -FR- corresponde a una parábola con vértice en el punto de coordenadas (1/A,B/A) sobre el plano varianza v.s. rendimiento. La siguiente instrucción dibuja ese punto con color rojo.
plot(1/A,B/A,'or')

El punto de coordenadas (1/A,B/A) señalado en la gráfica, corresponde al portafolio con menor riesgo que podemos encontrar entre todos los portafolios factibles que podemos formar con los activos del mercado bajo estudio. El cociente B/A nos dice el rendimiento correspondiente a dicho portafolio y el cociente 1/A su varianza.
El usuario debe intorducir el rendimiento del portafolio óptimo que le interesa seleccionar. Para efectos de este tutorial, asignaremos el valor predeterminado:
r=0.4;
Observamos que esta cantidad debe estar dentro de el rango apropiado para los rendimientos de los activos involucrados. En este caso lo hemos fijado como el doble del retorno máximo observado:
2*max(R)
ans =
0.4065
Tomando el valor r=0.4 como el rendimiento del portafolio óptimo que nos interesa, podemos dibujar su posición sobre la frontera eficiente utilizando la fórmula -FR-.
plot((A*r^2-2*B*r+C)/D,r,'om')
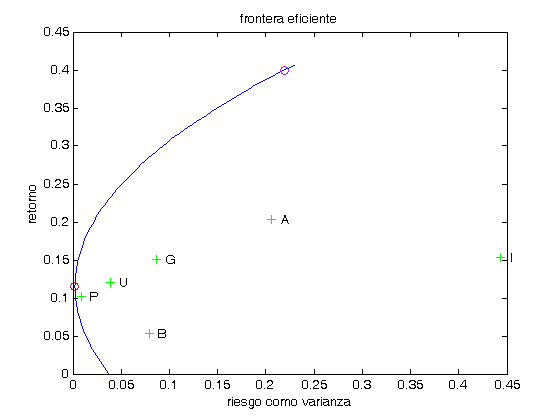
close
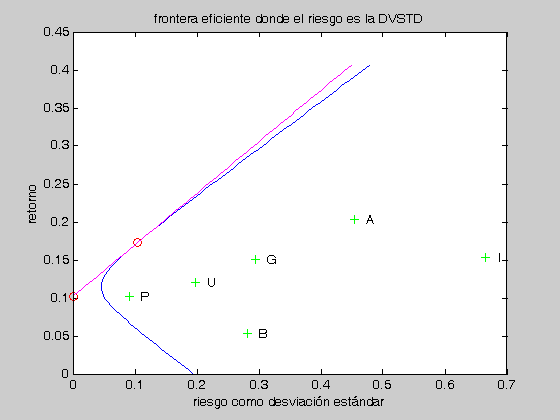
Aquí dibujaremos la frontera eficiente empleando la desviación estándar como medida de riesgo. Para ello tomamos la raíz cuadrada de la función cuadrática dada en la expresión -FR-. Como estamos evaluando raíces cuadradas, tendremos un poco de precaución y revisaremos que los argumentos sean simepre valores positivos.
for i=1:100 if (A*x(i)^2-2*B*x(i)+C)/D>0 z(i)=sqrt((A*x(i)^2-2*B*x(i)+C)/D); else z(i)=0; end end plot(z,x) hold on xlabel('riesgo como desviación estándar') ylabel('retorno') title('frontera eficiente donde el riesgo es la DVSTD')
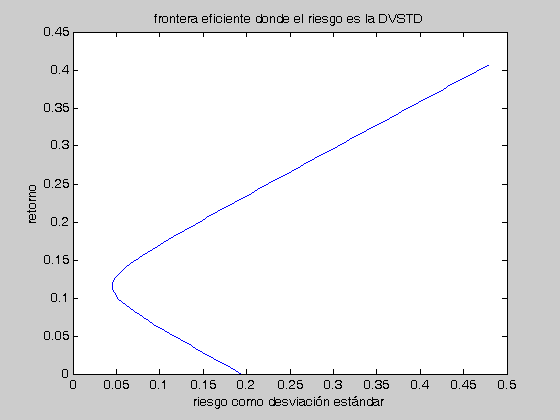
Ahora dibujaremos los activos en el mismo diagrama de desviación estándar v.s. retorno. Note que la desviación estándar de cada uno de ellos la obtenemos tomando la ráiz cuadrada de sus varianzas, las cuales a su vez aparecen en la diagonal de la matriz de covarianzas.
for i=1:6 plot(sqrt(S(i,i)),R(i),'+g') text(sqrt(S(i,i))+0.02,R(i),DTA(i)) end

La Teoría de la Cartera nos ofrece ventajas muy importantes para responder preguntas concretas en finanzas. En concreto, si nos proponen una tasa de interés determinada, podemos encontrar el portafolio de mercado que le corresponde, empleando la regla de tangencia que debe cumplir dicho portafolio. Esta regla de tangencia se describe de una manera muy cómoda a través de la siguiente relación lineal:
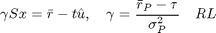
de manera que si nos proporcionan la tasa de interés $\tau$, podemos encontrar los valores para el portafolio de mercado correspondiente. Basta utilizar las siguientes fórmulas, que se obtienen fácilmente de las ecuaciones en -RL-.

Empleando estas fórmulas, calcularemos el rendimiento y la varianza del portafolio de mercado (portafolio óptimo) en función de la tasa de interés dada:
tasa=0.102; retorno=(C-tasa*B)/(B-tasa*A) varianza=(retorno-tasa)/(B-tasa*A) desviacion=sqrt(varianza)
retorno =
0.1726
varianza =
0.0108
desviacion =
0.1041
Dibujamos aquí, con rojo, el punto correspondiente a la tasa de interés sobre el eje de rendimiento. Cuidamos que el valor calculado para el retorno del portafolio de mercado sea mayor al de la tasa dada, porque en caso contrario no nos encontramos en el rango de valores posibles para utilizar como tasas de interés. Esto se debe a que la pendiente de la frontera eficiente tiene dos asíntotas cuando se representa sobre el plano de retorno v.s. desviación estándar.
plot(0,tasa,'or') if retorno>tasa plot(desviacion,retorno,'or') else plot(0,tasa,'om') end

Dibujaremos ahora la línea de mercado de capital que une a la tasa de interés dada, sobre el eje retorno, con el punto del portafolio de mercado, que se encuentra sobre la frontera eficiente. Note que esta línea es tangente a la frontera eficiente justamente en el punto que corresponde al portafolio de mercado. Esta condición geométrica es la definición alternativa para los portafolios eficientes, además es la guía para obtener las condiciones de primer orden dadas en la expresión -RL-.
w=(x-tasa)*(desviacion)/(retorno-tasa); for i=1:100 if w(i)<0 w(i)=0; end end plot(w,x,'m')
close
Es importante conocer, no sólamente la ubicación del portafolio de mercado en el diagrama riesgo v.s. rendimiento, sino que además nos interesa conocer el conjunto de inversiones que lo definen. Para ello debemos utilizar las fórmulas -SL- y -ML- para los multiplicadores de Lagrange, obteniendo la expresión:
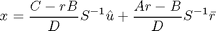
o alternativamente la condición de primer orden -RL- que nos proporciona la solución:
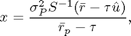
con la cual podemos implementar las instrucciones que dejan en la variable optimos el vector de las inversiones que componen el portafolio de mercado.
optimos1=(inv(S)*(R-tasa*u))*varianza/(retorno-tasa) optimos2=(inv(S)*u)*(C-B*retorno)/D+(inv(S)*R)*(A*retorno-B)/D
optimos1 =
0.2204
-0.7752
-0.2624
0.1085
0.8108
0.8979
optimos2 =
0.2204
-0.7752
-0.2624
0.1085
0.8108
0.8979
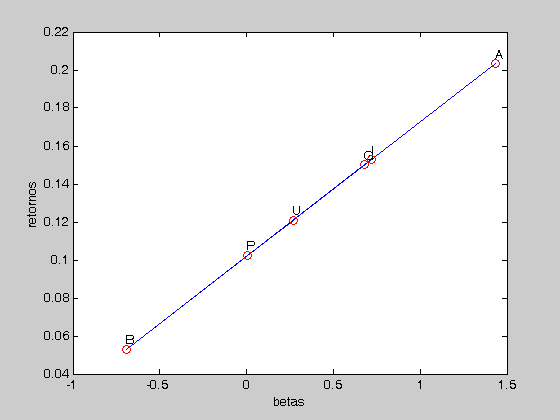
Para calcular los betas correspondientes a cada activo, utilizamos la definición básica:

que da lugar a las siguientes instrucciones:
beta=(R-tasa)/(retorno-tasa); plot(beta,R); text(beta,R+0.005,DTA); hold on for i=1:6 plot(beta(i),R(i),'or') end xlabel('betas') ylabel('retornos')

close
Como una forma alternativa para estimar los betas, podemos utilizar la definición:
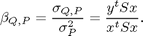
De esta manera implemementamos las siguientes operaciones:
for i=1:6 activo=zeros(1,6); activo(i)=1; beta(i)=activo*S*optimos1/varianza; end plot(beta,R); text(beta,R+0.005,DTA); hold on for i=1:6 plot(beta(i),R(i),'or') end xlabel('betas') ylabel('retornos')
close
Una labor muy importante en finanzas es proponer tasas de interés a partir de la información de un portafolio de mercado. Para ello tomaremos el nivel de redimiento r=0.25
r=0.25;
con el cual estimaremos la desviación estándar del portafolio, utilizando la raíz cuadrada de la fórmula -FR-:
desviacion=sqrt((A*r^2-2*B*r+C)/D)
desviacion =
0.2250
Dibujaremos la frontera eficiente, pero empleando la desviación estándar como medida de riesgo:
for i=1:100 if (A*x(i)^2-2*B*x(i)+C)/D>0 z(i)=sqrt((A*x(i)^2-2*B*x(i)+C)/D); else z(i)=0; end end plot(z,x) hold on xlabel('riesgo como desviación estándar') ylabel('retorno') title('frontera eficiente donde la desviación estándar mide al riesgo')
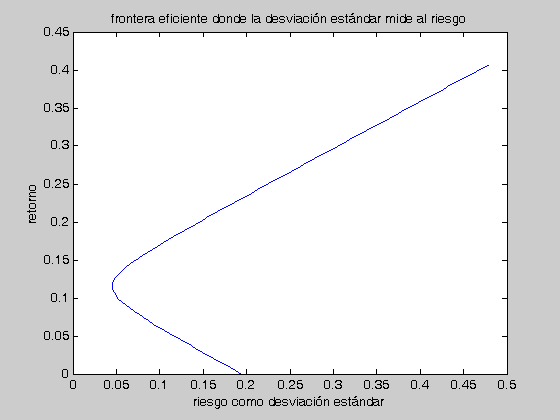
Utilizando la fórmula del rendimiento ótpimo -RO-, podemos hallar la tasa de interés:

de manera que podemos utilizar la siguiente instrucción para estimar la tasa de interes:
tasa=(r*B-C)/(r*A-B)
tasa =
0.1097
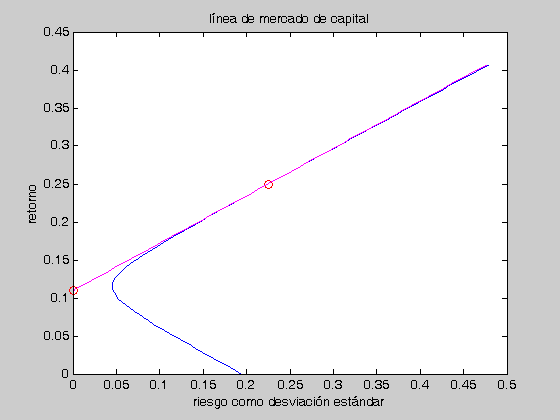
correspondiente al portafolio de mercado
[r,desviacion]
ans =
0.2500 0.2250
Sobre la frontera eficiente dibujaremos la línea de mercado de capital, señalaremos la tasa de interés calculada y el portafolio de mercado propuesto por el usuario.
w=(x-tasa)*(desviacion)/(r-tasa); for i=1:100 if w(i)<0 w(i)=0; end end plot(w,x,'m') plot(desviacion,r,'or') plot(w,x,'m') plot(0,tasa,'or') title('línea de mercado de capital')