Black Scholes

Modelo Matemático cuyo fin es estimar el valor hoy de una opcion europea para la compra (Call) o venta (Put), de acciones en una fecha futura. *(Consultar Bibliografía). Se desea desarrollar la ecuación diferencial:

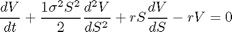
En donde:

r es la variable que representa la tasa de interés

r=0.0012;

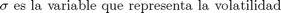
sigma=0.0003;

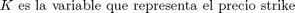
K=1630;

Sinf es la variable que representa el precio máximo numérico

Sinf=2000;

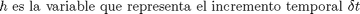
h=0.4;

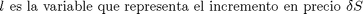
l=2;
% parámetros auxiliares

Análisis Matemático

El método numérico del cual se va a hacer uso para resolver la ecuación diferencial se llama diferencias finitas (ver bibliografía)

Desarrollo de los diferenciales:

Debemos transformar la ecuación diferencial para construir la matriz. Por lo tanto:

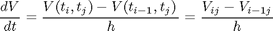
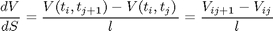
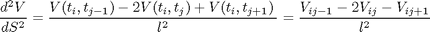
Reemplazando en la ecuación diferencial obtenemos:

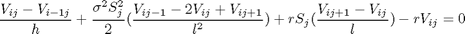
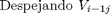
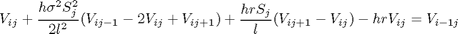
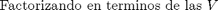
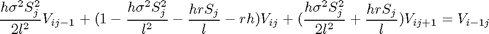
Creación de la matriz

Primero notamos que es una matriz cuadrada y que su tamaño esta determinado por el precio máximo dividido la longitud de los intervalos menos los valores extremos que por condiciones de frontera ya tenemos.

tamano=Sinf/l - 1;
%

Matriz

Usamos variables adicionales para una representación grafica de la ecuación más sencilla:

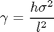
gama=h*sigma^2/l^2;

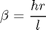
beta=h*r/l;
%

Iniciamos la Matriz de tamaño 'tamano' pues en este punto omitimos los extremos ya que por las condiciones iniciales tenemos esa información.

A=zeros(tamano,tamano);

Nos disponemos a ingresar los valores en la matriz con los datos correspondientes. Se inicia un ciclo desde la posición 2 y hasta la posición 'tamano-1' porque son las posiciones

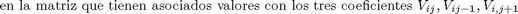
for j=2:(tamano-1)

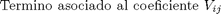
    A(j,j)=1-gama*(j*l)^2 - beta*l*j-beta*l;

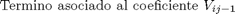
    A(j,j-1)=gama*(j*l)^2/2;

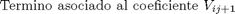
    A(j,j+1)=gama*(j*l)^2/2 + beta*l*j;

end

Para terminar de completar la matriz llenamos las posiciones huecas que hicieron falta manualmente. Primero con la primera posición

j=1;

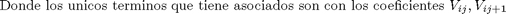
A(j,j)=1-gama*(j*l)^2 - beta*l*j-beta*l;
A(j,j+1)=gama*(j*l)^2/2 + beta*l*j;

Ahora la Ultima posición

j=tamano;
%

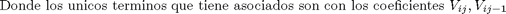
A(j,j)=1-gama*(j*l)^2 - beta*l*j-beta*l;
A(j,j-1)=gama*(j*l)^2/2;
%

Para completar el sistema lineal, construimos el vector columna b

b=zeros(tamano,1);
% Llenamos la información del vector, que en este caso solo contiene información en la primera posición.
b(1)=-gama*K/2;
%

Para terminar creamos el vector 'solución'

for j=1:999
    v(j,1)=max(0,K-j*l);
end
%

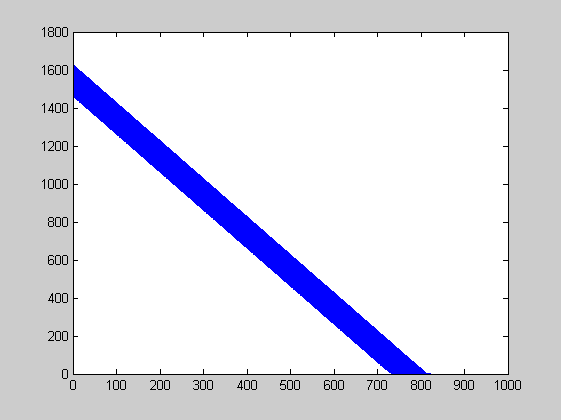
Dibujamos el vector y activamos en Matlab el comando para sobrescribir graficas.

plot(v);
hold on
% Iteramos el vector 225 veces.
for i=1:225
    v=A*v+b;
    plot(v)
end

Bibliografía

Wilmott Paul, Option Pricing: Mathematical models and computation, Oxford Financial Express 2000 Burden Richard, Análisis Numérico, Thomson Learning 2002

Wikipedia: http://es.wikipedia.org/wiki/Black-Scholes

Contents

MATEMÁTICAS FINANCIERAS