La curva que describe un cable que está fijo por sus dos extremos y no está sometido a otras fuerzas distintas que su propio peso es una catenaria. La catenaria se confundió al principio con la parábola, hasta que el problema lo resolvieron los hermanos Bernoulli simultáneamente con Leibniz y Huygens.
Formulación discreta
Sea una cadena de bolitas metálicas como las que se utilizan para sujetar los tapones de los fregaderos. Supondremos que hay N bolitas igualmente repartidas sobre un hilo de longitud L y de masa despreciable.
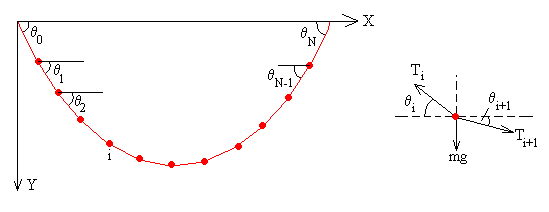
Cada bolita estará, por tanto, sometida a tres fuerzas: su propio peso, la fuerza que ejerce el hilo a su izquierda y a su derecha.
La condición de equilibrio para la bolita i de masa m se expresa
Todas las componentes horizontales de la tensión del hilo son iguales, y la denominaremos Tx.
Tx=Tcosq0= Tcosqi= Tcosqi+1 =TcosqN+1Dividiendo la segunda ecuación por Tx tenemos la siguiente relación entre el ángulo q i y el ángulo q i+1
A la cantidad constante cociente entre el peso de cada bolita mg y la componente horizontal Tx de la tensión del hilo, le denominaremos parámetro g . La relación de recurrencia se escribe para cada bolita i=1... N.
tanq1=tanq0-g
tanq2=tanq1-g
tanq3=tanq2-g
...............
tanqi=tanqi-1-g
.............
tanqN-1=tanqN-2-g
tanqN=tanqN-1-g
Sumando miembro a miembro obtenemos el ángulo qN en función del ángulo inicial q0.
tanqN=tanq0-Ng
Si los extremos del hilo están a la misma altura, por razón de simetría tendremos quetanq0=- tanqNPor tanto, tanq0=Ng /2Sumando miembro a miembro la relación de recurrencia hasta el término i, obtenemos el ángulo qi en función del ángulo inicial q0.tanqi=tanq0-g i=(N-2i)·g /2El ángulo qi que forma el hilo con la horizontal en la posición de cada una de las bolitas, el ángulo inicial q0 y el final qN se calculan mediante la siguiente fórmula
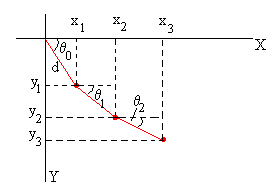
Las coordenadas (xi, yi) de la bolita i se obtendrán sumando las proyecciones d·cosq j y d·senq j, j=0...i-1, sobre el eje X y sobre el eje Y respectivamente, siendo d la distancia entre dos bolitas consecutivas d=L/(N+1)
 |
 |
Derivando con respecto de x, y teniendo en cuenta que la longitud del arco diferencial ds2=dx2+dy2
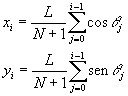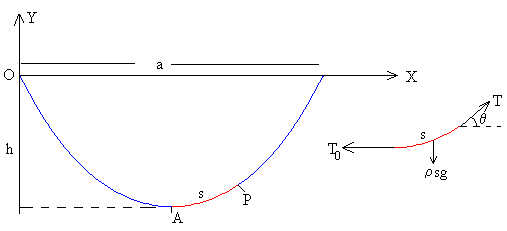
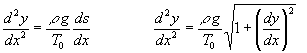(1)Integrando esta ecuación, teniendo en cuenta que para x=a/2, (en el punto más bajo A de la curva) dy/dx=0.
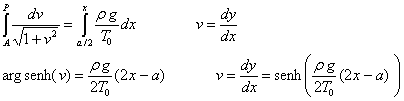Integrando de nuevo, con la condición de que para x=a/2, y=-h.
Como la catenaria es simétrica para x=a, y=0, por lo que la flecha h vale.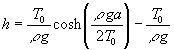
La ecuación de la catenaria es, finalmente
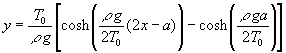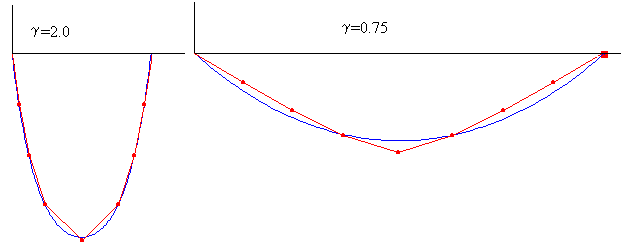
(2)La longitud de la catenaria es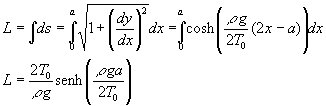
(3)Las figuras, son una superposición de las imágenes generadas por los dos applets de esta página que muestran como la aproximación discreta y continua coinciden cuando el parámetro g es grande y difieren cuando g es pequeño. El parámetro g=mg/Tx es el cociente entre el peso de cada bolita y la componente horizontal de la tensión del hilo, que es la misma en cada una de las bolitas.
