• 2.1.Introducción
• 2.2.Definiciones
  • 2.2.1Ecuación Algebráica Lineal
  • 2.2.2Sistema de Ecuaciones
  • 2.2.3Solución de un Sistema de Ecuaciones
• 2.3.Teorema de Rangos
• 2.4.Eliminación Gaussiana
  • 2.4.1Desventajas del Método
• 2.5Método de Gauss - Jordan
  • 5.1Inversión de Matrices
• 2.6.Método de Gauss - Seidel

2.1. INTRODUCCIÓN

En las distintas ramas de la ingeniería se plantean problemas en que se hace necesario resolver sistemas de ecuaciones lineales simultáneas con un número bastante grande de ecuaciones como para resolverlo manualmente o con calculadora, por lo que hemos de conocer algunos métodos directos e iterativos fáciles de programar para resolverlos con ayuda de la computadora.

OBJETIVOS

1. Comprender y aplicar fluidamente, los métodos para resolver un sistema de ecuaciones lineales simultáneas por cumputadora.
   • Métodos Directos
     • Eliminación de Gauss-Jordan
     • Inversión de matrices
   • Métodos Iterativos
     • Gauss-Seidel
2. Diferenciar las ventajas y desventajas de cada uno de los métodos.

2.2. DEFINICIONES

2.2.1 ECUACIÓN ALGEBRÁICA LINEAL

Es aquella en donde en cada término de la ecuación aparece únicamente una variable o incógnita elevada a la primera potencia. Por ejemplo:

Es una ecuación algebraica lineal en las variables X1, X2, X3, ... , Xn. Se admite que los coeficientes a11, a12, a13, ... , a1n y el término independiente C1, son constantes reales.

2.2.2 SISTEMA DE ECUACIONES

Es un conjunto de ecuaciones que deben resolverse simultáneamente. En los sucesivo se considerarán únicamente sistemas de ecuaciones algebráicas lineales, o sea conjuntos de ecuaciones de la forma:

Aplicando la definición de producto entre matrices, este sistema de n ecuaciones algebraicas lineales con n incógnitas puede escribirse en forma matricial.

(3)

Este sistema de ecuaciones puede escribirse simbólicamente como:

en donde A se llama Matriz del Sistema. La matriz formada por A, a la que se le ha agregado el vector de términos independientes como última columna, se le llama la Matriz Ampliada del Sistema, que se representa con (A, C).

Entonces la matriz ampliada será:

(5)

2.2.3 SOLUCIÓN DE UN SISTEMA DE ECUACIONES

Es un conjunto de valores de las incógnitas que verifican simultáneamente a todas y cada una de las ecuaciones del sistema.

De acuerdo con su solución, un sistema puede ser: Consistente, si admite solución; o Inconsistente, si no admite solución.

Un sistema Consistente puede ser: Determinado, si la solución es única o Indeterminado, si la solución no es única. En este caso se demuestra que existe una infinidad de soluciones.

2.3. TEOREMAS SOBRE RANGOS

El rango de una matriz es el orden de determinante no nulo de mayor orden que puede obtenerse de esa matriz. El rango de la matriz A se representa con la notación r(A) y el de la matriz ampliada con r(A, C).

En álgebra se demuestra que:

1. Para cualquier sistema,
2. Si r(A) < r(A, C) el sistema es inconsistente
3. Si r(A) = r(A, C) el sistema de ecuaciones es consistente

En este caso, si además r(A) = n, el sistema es determinado e indeterminado si r(A) < n, siendo n el número de variables en el sistema.

En general, hay dos tipos de técnicas numéricas para resolver ecuaciones simultáneas: Directas, que son finitas; e Indirectas, que son infinitas.

Naturalmente, ninguna técnica práctica puede ser infinita. Lo que queremos decir es que en un principio los métodos directos (despreciando errores por redondeo) producirán una solución exacta, si la hay, en un número finito de operaciones aritméticas.

Por otra parte, un método indirecto requerirá en principio un número infinito de operaciones aritméticas para producir una solución exacta. Dicho de otra manera, un método indirecto tiene un error por truncamiento mientras que un método directo no lo tiene.

Sin embargo, la expresión "en principio" del párrafo anterior es crucial: en realidad se tienen errores por redondeo. Tendremos que considerar más cuidadosamente esta cuestión. En un sistema grande, mal comportado, los errores por redondeo de un método directo puede hacer que la "solución" carezca de sentido. A pesar de su error teórico por truncamiento, un método indirecto puede ser mucho más deseable porque en él los errores por redondeo no se acumulan.

2.4. MÉTODO DE ELIMINACIÓN DE GAUSS

El primer método que se presenta usualmente en álgebra, para la solución de ecuaciones algebricas lineales simultáneas, es aquel en el que se eliminan las incógnitas mediante la combinación de las ecuaciones. Este método se conoce como Método de Eliminación. Se denomina eliminación Gaussiana si en el proceso de eliminación se utiliza el esquema particular atribuido a Gauss. Utilizando el método de Gauss, un conjunto de n ecuaciones con n incógnitas se reduce a un sistema triangular equivalente (un sistema equivalente es un sistema que tiene iguales valores de la solución), que a su vez se resuelve fácilmente por "sustitución inversa"; un procedimiento simple que se ilustrará con la presentación siguiente.

El esquema de Gauss empieza reduciendo un conjunto de ecuaciones simultáneas, tal como se muestra en (2), a un sistema triangular equivalente como:

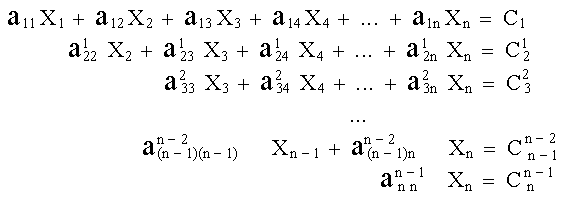(6)

en el cual los superíndices indican los nuevos coeficientes que se forman en el proceso de reducción. La reducción real se logra de la siguiente manera:

1. La primera ecuación (2) se divide entre el coeficiente de X1 en esa ecuación para obtener:

   (7)

   La ec. (7) se multiplica entonces por el coeficiente de X1 de la segunda ecuación (2) y la ecuación que resulta se resta de la misma, eliminando así X1. La ec. (7) se multiplica entonces por el coeficiente de X1 de la tercera ecuación (2), y la ecuación resultante se resta de la misma para eliminar X1 de esa ecuación. En forma similar, X1 se elimina de todas las ecuaciones del conjunto excepto la primera, de manera que el conjunto adopta la forma:

   (8)

   La ecuación utilizada para eliminar las incógnitas en las ecuaciones que la siguen se denomina Ecuación Pivote. En la ecuación pivote, el coeficiente de la incógnita que se va a eliminar de las ecuaciones que la siguen se denomina el Coeficiente Pivote (a11 en los pasos previos).

2. Siguiendo los pasos anteriores, la segunda ecuación (8) se convierte en la ecuación pivote, y los pasos de la parte 1 se repiten para eliminar X2 de todas las ecuaciones que siguen a esta ecuación pivote.

   Esta reducción nos conduce a:

   (9)

3. A continuación se utiliza la tercer ecuación (9) como ecuación pivote, y se usa el procedimiento descrito para eliminar X3 de todas las ecuaciones que siguen a la tercer ecuación (9). Este procedimiento, utilizando diferentes ecuaciones pivote, se continúa hasta que el conjunto original de ecuaciones ha sido reducido a un conjunto triangular tal como se muestra en la ec. (6).

4. Una vez obtenido el conjunto triangular de ecuaciones, la última ecuación de este conjunto equivalente suministra directamente el valor de Xn (ver ec. 6). Este valor se sustituye entonces en la antepenúltima ecuación del conjunto triangular para obtener un valor de Xn-1, que a su vez se utiliza junto con el valor de Xn en la penúltima ecuación del conjunto triangular para obtener un valor Xn-2 y asi sucesivamente. Este es el procedimiento de sustitución inversa al que nos referimos previamente.

Para ilustrar el método con un conjunto numérico, apliquemos estos procedimientos a la solución del siguiente sistema de ecuaciones:

Utilizando como ecuación pivote la primera ecuación (el coeficiente pivote es unitario), obtenemos:

A continuación, utilizando la segunda ecuación del sistema (11) como ecuación pivote y repitiendo el procedimiento, se obtiene el siguiente sistema triangular de ecuaciones:

Finalmente mediante sustitución inversa, comenzando con la última de las ecs. (12) se obtienen los siguientes valores:

2.4.1 DESVENTAJAS DEL MÉTODO DE ELIMINACIÓN

1. DIVISIÓN ENTRE CERO

   Una de sus desventajas es que durante el proceso en las fases de eliminación y sustitución es posible que ocurra una división entre cero. Se ha desarrollado una estrategia del pivoteo para evitar parcialmente estos problemas. Ésta se deja como investigación al alumno.

2. ERRORES DE REDONDEO

   La computadora maneja las fracciones en forma decimal con cierto número limitado de cifras decimales, y al manejar fracciones que se transforman a decimales que nunca terminan, se introduce un error en la solución de la computadora. Este se llama error por redondeo.

   Cuando se va a resolver solamente un pequeño número de ecuaciones, el error por redondeo es pequeño y generalmente no se afecta sustancialmente la presición de los resultados, pero si se van a resolver simultáneamente muchas ecuaciones, el efecto acumulativo del error por redondeo puede introducir errores relativamente grandes en la solución. Por esta razón el número de ecuaciones simultáneas que se puede resolver satisfactoriamente con el método de eliminación de Gauss, utilizando de 8 a 10 dígitos significativos en las operaciones aritméticas, se limita generalmente a 15 o 20.

3. SISTEMAS MAL CONDICIONADOS

   La obtención de la solución depende de la condición del sistema. En sentido matemático, los sistemas bien condicionados son aquellos en los que un cambio en uno o más coeficientes provoca un cambio similar en la solución. Los sistemas mal condicionados son aquellos en los que cambios pequeños en los coeficientes provocan cambios grandes en la solución.

   Una interpretación diferente del mal condicionamiento es que un rango amplio de respuestas puede satisfacer aproximadamente al sistema. Ya que los errores de redondeo pueden inducir cambios pequeños en los coeficientes, estos cambios artificiales pueden generar errores grandes en la solución de sistemas mal condiconados.

2.5. MÉTODO DE GAUSS - JORDAN

Este método, que constituye una variación del método de eliminación de Gauss, permite resolver hasta 15 o 20 ecuaciones simultáneas, con 8 o 10 dígitos significativos en las operaciones aritméticas de la computadora. Este procedimiento se distingue del método Gaussiano en que cuando se elimina una incógnita, se elimina de todas las ecuaciones restantes, es decir, las que preceden a la ecuación pivote así como de las que la siguen.

El método se ilustra mejor con un ejemplo. Resolvamos el siguiente conjunto de ecuaciones

Primero expresemos los coeficientes y el vector de términos independientes como una matriz aumentada.

Se normaliza el primer renglón dividiendo entre 3 para obtener:

El término X1 se puede eliminar del segundo renglón restando 0.1 veces el primero del segundo renglón. De una manera similar, restando 0.3 veces el primero del tercer renglón se elimina el término con X1 del tercer renglón.

En seguida, se normaliza el segundo renglón dividiendo entre 7.00333:

Reduciendo los términos en X2 de la primera y la tercera ecuación se obtiene:

El tercer renglón se normaliza dividiendolo entre 10.010:

Finalmente, los términos con X3 se pueden reducir de la primera y segunda ecuación para obtener:

Nótese que no se necesita sustitución hacia atrás para obtener la solución.

Las ventajas y desventajas de la eliminación gaussiana se aplican también al método de Gauss-Jordan.

Aunque los métodos de Gauss-Jordan y de eliminación de Gauss pueden parecer casi idénticos, el primero requiere aproximadamente 50% menos operaciones. Por lo tanto, la eliminación gaussiana es el mé todo simple por excelencia en la obtención de soluciones exactas a las ecuaciones lineales simultáneas. Una de las principales razones para incluir el método de Gauss-Jordan, es la de proporcionar un método directo para obtener la matriz inversa.

2.5.1 INVERSIÓN DE MATRICES

Sea A una matriz cuadrada no singular, es decir, que su determinante sea diferente de cero, . Por definición de matriz inversa, se tiene que

es la inversa de A si:

(13)

Haciendo y sustituyendo en la ecuación anterior, se obtiene

Puede considerarse que esta ecuación matricial representa un sistema de ecuaciones simultáneas, en donde no hay un solo vector de términos independientes sino n, los n vectores básicos que forman la matriz unitaria I. Además, no existe un solo vector de incógnitas, sino n, los que corresponden a cada columna de la matriz unitaria.

Por lo anterior, es posible determinar la inversa de una matriz con el método de Gauss-Jordan de eliminación completa. Para lograrlo, bastará con aplicar las operaciones elementales sobre los renglones de la matriz ampliada (A, I) de manera de transformar A en I. Cuando se haya hecho, se obtendrá la matriz ampliada , con lo que se tendrá la inversa buscada.

EJEMPLO

Invertir la matriz

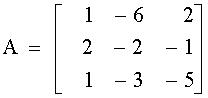
Auméntese la matriz de coeficientes con una matriz identidad

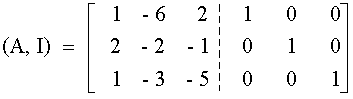
Usando a11 como pivote, el renglón 1 se normaliza y se usa para eliminar a X1 de los otros renglones.

En seguida, se usa a22 como pivote y X2 se elimina de los otros renglones.

Finalmente, se usa a33 como pivote y X3 se elimina de los renglones restantes:

Por lo tanto, la inversa es:

Se puede resolver un sistema de ecuaciones con la inversa de la matriz de coeficientes, de la siguiente manera:

donde C es el vector de términos independientes.

Comparando ambos métodos, es evidente que el método de inversión de matrices no es práctico para la solución de un sólo conjunto (o dos o tres conjuntos) de ecuaciones simultáneas, porque la cantidad de cálculos que intervienen para determinar la matriz inversa es muy grande. Sin embargo, si se desea resolver 20 conjuntos de 10 ecuaciones simultáneas que difieren únicamente en sus términos independientes, una matriz aumentada que contiene 20 columnas de constantes (que se utilizarían en el método de eliminación) sería difícil de reducir, y se podría usar con ventaja el método de inversión de matrices.

2.6. MÉTODO DE GAUSS-SEIDEL

Sin embargo, existen varias técnicas que se pueden utilizar, para resolver grandes números de ecuaciones simultáneas. Una de las técnicas más útiles es el método de Gauss-Seidel. Ninguno de los procedimientos alternos es totalmente satisfactorio, y el método de Gauss-Seidel tiene la desventaja de que no siempre converge a una solución o de que a veces converge muy lentamente. Sin embargo, este método convergirá siempre a una solución cuando la magnitud del coeficiente de una incógnita diferente en cada ecuación del conjunto, sea suficientemente dominante con respecto a las magnitudes de los otros coeficientes de esa ecuación. Es difícil definir el margen mínimo por el que ese coeficiente debe dominar a los otros para asegurar la convergencia y es aún más difícil predecir la velocidad de la convergencia para alguna combinación de valores de los coeficientes cuando esa convergencia existe. No obstante, cuando el valor absoluto del coeficiente dominante para una incógnita diferente para cada ecuación es mayor que la suma de los valores absolutos de los otros coeficientes de esa ecuación, la convergencia está asegurada. Ese conjunto de ecuaciones simultáneas lineales se conoce como sistema diagonal. Un sistema diagonal es condición suficiente para asegurar la convergencia pero no es condición necesaria. Afortunadamente, las ecuaciones simultáneas lineales que se derivan de muchos problemas de ingeniería, son del tipo en el cual existen siempre coeficientes dominantes.

La secuencia de pasos que constituyen el método de Gauss-Seidel es la siguiente:

1. Asignar un valor inicial a cada incógnita que aparezca en el conjunto. Si es posible hacer una hipótesis razonable de éstos valores, hacerla. Si no, se pueden asignar valores seleccionados arbitrariamente. Los valores iniciales utilizados no afectarán la convergencia como tal, pero afectarán el número de iteraciones requeridas para dicha convergencia.

2. Partiendo de la primera ecuación, determinar un nuevo valor para la incógnita que tiene el coeficiente más grande en esa ecuación, utilizando para las otras incógnitas los valores supuestos.

3. Pasar a la segunda ecuación y determinar en ella el valor de la incógnita que tiene el coeficiente más grande en esa ecuación, utilizando el valor calculado para la incógnita del paso 2 y los valores supuestos para las incógnitas restantes.

4. Continuar con las ecuaciones restantes, determinando siempre el valor calculado de la incógnita que tiene el coeficniente más grande en cada ecuación particular, y utilizando siempre los últimos valores calculados para las otras incógnitas de la ecuación. (Durante la primera iteración, se deben utilizar los valores supuestos para las incógnitas hasta que se obtenga un valor calculado). Cuando la ecuación final ha sido resuelta, proporcionando un valor para la única incógnita, se dice que se ha completado una iteración.

5. Continuar iterando hasta que el valor de cada incógnita, determinado en una iteración particular, difiera del valor obtenido en la iteración previa, en una cantidad menor que cierto seleccionado arbitrariamente. El procedimiento queda entonces completo.

Refiriéndonos al paso 5, mientras menor sea la magnitud del seleccionado, mayor será la precisión de la solución. Sin embargo, la magnitud del epsilon no especifica el error que puede existir en los valores obtenidos para las incógnitas, ya que ésta es una función de la velocidad de convergencia. Mientras mayor sea la velocidad de convergencia, mayor será la precisión obtenida en los valores de las incógnitas para un dado.

EJEMPLO

Resolver el siguiente sistema de ecuación por el método Gauss-Seidel utilizando un = 0.001.

SOLUCIÓN:

Primero ordenamos las ecuaciones, de modo que en la diagonal principal esten los coeficientes mayores para asegurar la convergencia.

Despejamos cada una de las variables sobre la diagonal:

Suponemos los valores iniciales X2 = 0 y X3 = 0 y calculamos X1

Este valor junto con el de X3 se puede utilizar para obtener X2

La primera iteración se completa sustituyendo los valores de X1 y X2 calculados obteniendo:

En la segunda iteración, se repite el mismo procedimiento:

Comparando los valores calculados entre la primera y la segunda iteración

Como podemos observar, no se cumple la condición

Entonces tomamos los valores calculados en la última iteración y se toman como supuestos para la siguiente iteración. Se repite entonces el proceso:

Comparando de nuevo los valores obtenidos

Como se observa todavía no se cumple la condición

Así que hacemos otra iteración

Comparando los valores obtenidos

Dado que se cumple la condición, el resultado es:

Como se puede comprobar no se tiene un número exacto de iteraciones para encontrar una solución. En este ejemplo, se hicieron 3 iteraciones, pero a menudo se necesitan más iteraciones.

Se deja de investigación al alumno alguna forma que haga que este método converga más rápidamente.