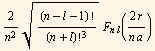
Densidad de probabilidad radial para estados 1s, 2s y 3s del átomo de Hidrogeno

La densidad de probabilidad radial está dada por
    P(r) = r^2R^2_ (n l)
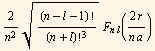
    R_ (n l) = a^(-3/2)2/n^2 (n - l - 1) !/(n + l) !^3^(1/2) F_ (n l)((2r)/(n a))
    F_ (n l)(x) = x^l ^(-x/2) L_ (n - l - 1)^(2l + 1)(x)
     L_q^p(x) = (p + q) ! LagerreL[p, q, x]

f[n_, l_, r_] := r^l ^(-r/2) (n + l) ! LaguerreL[n - l - 1, 2l + 1, r] ; funrad[n_, l_, r_] := (2 a^(-3/2) )/n^2 (n - l - 1) !/(n + l) !^3^(1/2) f[n, l, (2r)/(n a)] ;

En unidades de radio de Bohr (a→ 1)

Plot[Table[(r funrad[i, 0, r])^2, {i, 3}]/.a1, {r, 0, 25}] ;

2 Plot :: plnr : Table[(r funrad[i, 0, r]) , {i, 3}]/.a1 is not a machine-size real number at r = 1.0416666666666667`*^-6. More…

2 Plot :: plnr : Table[(r funrad[i, 0, r]) , {i, 3}]/.a1 is not a machine-size real number at r = 1.014174789322895`. More…

2 Plot :: plnr : Table[(r funrad[i, 0, r]) , {i, 3}]/.a1 is not a machine-size real number at r = 2.1202199964843422`. More…

General :: stop : Further output of Plot :: plnr will be suppressed during this calculation. More…

[Graphics:../HTMLFiles/graficas_243.gif]

Plot[Evaluate[Table[(r funrad[i, 0, r])^2, {i, 3}]/.a1], {r, 0, 25}, PlotRange {0, 0.6}, AxesLabel {"r(a)", "P(r) (1/a)"}] ;

[Graphics:../HTMLFiles/graficas_245.gif]

Plot[Evaluate[Table[(r funrad[i, 0, r])^2, {i, 3}]/.a1], {r, 0, 25}, PlotRange ... g[{.01, .02}]},  {GrayLevel[.5],   Thickness[.009], Dashing[{.02}]} }] ;

[Graphics:../HTMLFiles/graficas_247.gif]

Clear[f, funrad] ;

Created by Mathematica  (August 6, 2004)