Cambio de entropía

El cambio de entropía entre los estadoa a y b de un sistema está dado por
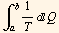
    ΔS = s_b - s_a=∫_a^b1/TQ
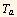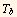donde T es la temperatura del sistema y dQ el diferencial de calor que entra o sale de este. La integral se evalúa sobre cualquier camino reversible que conecta los dos estados. Para procesos que se dan a presión constante y la temperatura cambia de T_aa T_b, la ecuación se puede escribir como
    s_b - s_a=∫_T_a^T_bC_p(T)/TT
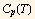donde C_p(T)es la capacidad calorífica del sistema a presión constante.
Determinar el cambio de temperatura para la siguiente tabla de datos se obtuvo para alguna sustancia
    T (K) 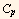       C_p (cal/K)    T (K)        C_p (cal/K)
    15        0.311        160        4.123
    20        0.605        170        4.269
    25        0.858        180        4.404
    30        1.075        190        4.526
    40        1.452        200        4.639
    50        1.772        210        4.743
    60        2.084        220        4.841
    70        2.352        230        4.927
    80        2.604        240        5.010
    90        2.838        250        5.083
    100        3.060        260        5.154
    110        3.254        270        5.220
    120        3.445        280        5.286
    130        3.624        290        5.350
    140        3.795        298.1        5.401
    150        3.964

Construir una lista para los valores de temperatura en Kelvin

In[3]:=

t = Table[i, {i, 20, 290, 10}]

Out[3]=

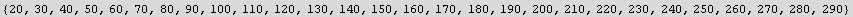
{20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290}

In[4]:=

t = Prepend[t, 15]

Out[4]=

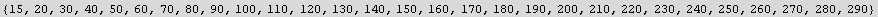
{15, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290}

In[5]:=

t = Insert[t, 25, 3]

Out[5]=

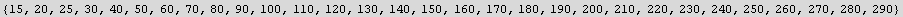
{15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290}

In[6]:=

t = Append[t, 298.1]

Out[6]=

{15, 20, 25, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210, 220, 230, 240, 250, 260, 270, 280, 290, 298.1}

Construir una lista para los valores de capacidad calorífica en cal/K

In[28]:=

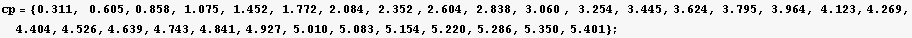
cp = {0.311,   0.605, 0.858, 1.075, 1.452, 1.772, 2.084, 2.352 , 2.604, 2.838, 3.06 ... , 4.269, 4.404, 4.526, 4.639, 4.743, 4.841, 4.927, 5.01, 5.083, 5.154, 5.22, 5.286, 5.35, 5.401} ;

Aproximamos la integral utilizando la regla del trapecio
    Underoverscript[∑, i = 1, arg3] (C_p(T_ (i + 1))/T_ (i + 1) + C_p(T_i)/T_i) ((T_ (i + 1) - T_i)/2)

In[29]:=

Underoverscript[∑, i = 1, arg3] ((t[[i + 1]] - t[[i]])/2 (cp[[i + 1]]/t[[i + 1]] + cp[[i]]/t[[i]]))

Out[29]=

7.50452

Podemos utilizar una función de un paquete para hacer integración numérica

In[12]:=

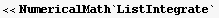
<<NumericalMath`ListIntegrate`

In[13]:=

? ListIntegrate

ListIntegrate[{y0, y1, ..., yn}, h, k] uses an InterpolatingFunction object of order k to give ... , you may be better off performing Integrate on the result of Fit applied to the data. More…

In[30]:=

ListIntegrate[Transpose[{t, cp/t}], 1] (*lineal*)

Out[30]=

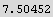
7.50452

In[31]:=

ListIntegrate[Transpose[{t, cp/t}]] (*cúbico*)

Out[31]=

7.51218

También podemos graficar C_p contra T

In[26]:=

? ListPlot

ListPlot[{y1, y2, ... }] plots a list of values. The x coordinates for each point are taken to ... {{x1, y1}, {x2, y2}, ... }] plots a list of values with specified x and y coordinates. More…

In[32]:=

ListPlot[Transpose[{t, cp}]] ;

[Graphics:../HTMLFiles/listas_286.gif]

In[34]:=

t=. cp=.

Created by Mathematica  (August 6, 2004)